[코딩 테스트 합격자 되기 - 9주차] 백트래킹(BackTracking)

완전 탐색 : 깊이 우선 탐색, 너비 우선 탐색과 같이 데이터를 전부 확인하는 탐색 방법을 의미한다. 

우리는 이 글에서 공부해 볼 탐색 방법은 백트래킹으로 지난 깊이 우선 탐색, 너비 우선 탐색을 공부하던 중 탐색 진행이 더이상 불가능해 졌을 때 되돌아 오는 것을 착안해서 가능성이 없는 곳에서는 되돌아 가고, 가능성이 있는 곳을 탐색하는 알고리즘이다. 

 

유망 함수

백트래킹 알고리즘의 핵심은 해가 될 가능성을 판단하는 것. 그리고 그 가능성은 유망 함수라는 것을 정의하여 판단한다. 

1. 유효한 해의 집합을 정의
2. 위 단계에서 정의한 집합을 그래프로 표현
3. 유망 함수 정의
4. 백트래킹 알고리즘을 활용해서 해를 찾음

유망 함수가 백트래킹 알고리즘에서 어떻게 동작하는지 예제를 통해 알아보자

합이 6이 넘는 조합 알아보기

{1, 2, 3, 4} 중 2개의 숫자를 뽑아 합이 6을 초과하는 경우를 알아내는 백트래킹 알고리즘을 알아보자. 이때 뽑는 순서가 다르면 다른 경우의 수로 간주한다. 

1. 유효한 해의 집합을 정의. 서로 다른 두 수를 뽑는 경우의 수는 다음과 같다.

   

2. 정의한 해의 집합을 그래프로 표현

   

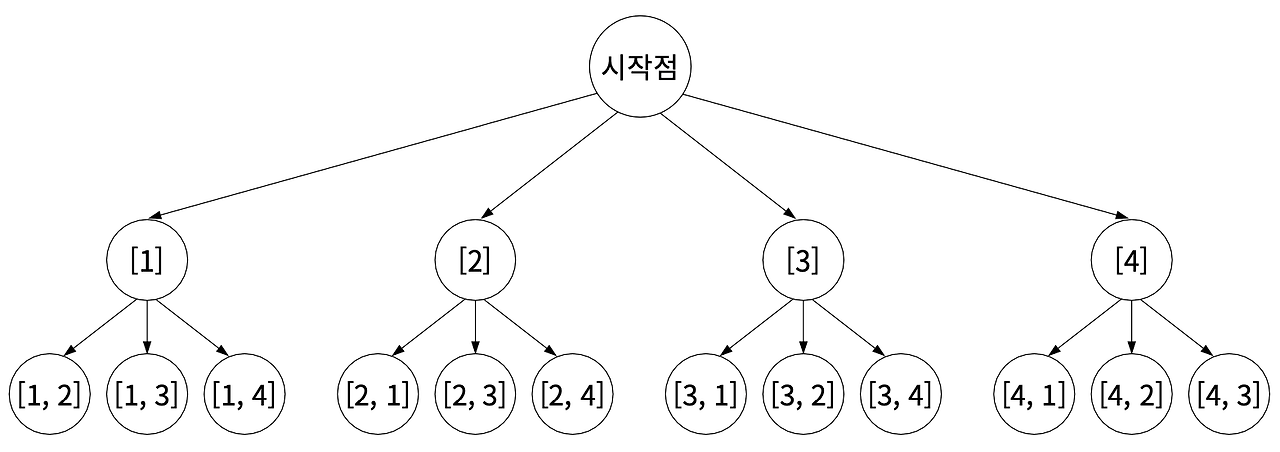
3. 그래프에서 백트래킹을 수행. 그림을 보면 처음에 오는 숫자가 2 이하인 경우에는 6을 초과할 수 있는 조합이 발생하지 않으므로 아예 탐색을 시도하지 않는다. 이러한 특정 조건을 유망 함수로 정의한다. 

   

4. 따라서 3은 유망 함수를 통과한다. 1, 2의 경우, 깊이 우선 탐색 알고리즘에 의해 방문은 하지만 답이 아니므로 백트래킹을 한다.

   

5. 이후도 동일하다.

   

N-Queens(프로그래머스 - 문제 링크)

def dfs(n, y, v1, v2, v3):
    ans = 0
    if y == n:  # N행까지 진행한 경우의 수 가능 : 성공
        ans += 1

    for j in range(n):
        if v1[j] == v2[y + j] == v3[y - j] == 0:  # 열 / 대각선 모두 Q 없음
            v1[j] = v2[y + j] = v3[y - j] = 1
            ans += dfs(n, y + 1, v1, v2, v3)
            v1[j] = v2[y + j] = v3[y - j] = 0

    return ans

def solution(n):
    v1 = [0] * n
    v2 = [0] * (2 * n)
    v3 = [0] * (2 * n)
    ans = dfs(n, 0, v1, v2, v3)
    return ans