[백준/파이썬][Gold III] 행렬 곱셈 순서 - 11049

[Gold III] 행렬 곱셈 순서 - 11049

문제 링크

성능 요약

메모리: 112952 KB, 시간: 540 ms

분류

다이나믹 프로그래밍

제출 일자

2025년 2월 10일 17:42:53

문제 설명

크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.

예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.

• AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
• BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.

같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.

행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다.

입력

첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 500)이 주어진다.

둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 500)

항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.

출력

첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 2³¹-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 2³¹-1보다 작거나 같다.

풀이

def main() :
    N = int(input())
    matrix = []
    for _ in range(N) :
        r, c = map(int, input().split())
        matrix.append((r, c))

    dp = [[(1<<32)] * N for _ in range(N)]

    for i in range(N) :
        dp[i][i] = 0

    for diagonal in range(1, N) :
        for i in range(N - diagonal) :  # 대각선의 우측 한 칸씩
            j = i + diagonal     # 현재 대각선에서 몇 번째 원소인지

            # 각 부분 행렬의 곱셈 횟수 + 두 행렬의 곱셈 횟수
            for k in range(i, j) :  # k값으로 최적분할 찾기
                dp[i][j] = min(dp[i][j],
                               dp[i][k] + dp[k+1][j] + matrix[i][0] * matrix[k][1] * matrix[j][1])


    print(dp[0][N-1])

main()

1. 동적 계획법(DP) 테이블 초기화

• DP 테이블 dp
  • dp[i][j]는 행렬 $A_{i} \times A_{i+1} \times \ldots \times A_{j}$ 를 계산할 때 필요한 최소 곱셈 연산 횟수를 저장
  • 2차원 리스트 DP 테이블 dp를 만들고 안의 요소를 모두 매우 큰 값으로 초기화
  • dp[i][i]는 곱셈 연산이 필요 없으므로 dp[i][i] = 0 으로 갱신

 

2. 구간별 최소 비용 계산 (DP 점화식)

• 구간 길이 diagonal를 기준으로 DP 계산
  • 외부 루프에서 diagonal은 현재 고려하는 행렬 연쇄의 길이를 나타냄
• 시작 인덱스 i와 종료 인덱스 j
  • i는 행렬 곱셈의 시작 인덱스, j = i + diagonal는 끝 인덱스
  • 모든 가능한 (i, j)에 대해 최소 비용을 구함
• 분할 위치 k
  • 연쇄 $A_{i} \ldots A_{j}$ 를 곱하는 최적 비용은
    $$dp[i][j] = \min_{i \leq k < j} {dp[i][k] + dp[k + 1][j] + matrix[i] \times matrix[k+1] \times matrix[j+1]} $$
  • 여기서 k는 연쇄를 두 부분으로 나누는 분할점
    • dp[i][k] : 왼쪽 부분 $A_{i} \ldots A_{k}$ 를 곱하는 최소 비용
    • dp[k+1][j] : 오른쪽 부분 $A_{k+1} \ldots A_{j} $ 를 곱하는 최소 비용
    • matrix[i] * matrix[k+1] * matrix[j+1] : 두 결과 행렬을 곱하는 데 필요한 연산 수
  • 가능한 모든 k에 대해 계산하여 최소 비용을 dp[i][j] 에 저장

 

3. 예제 분석

• A : $5 \times 3$
• B : $3 \times 2$
• C : $2 \times 6$

1. diagonal = 1

• 구간 (0, 1) : $A \times B$
  • i=0, j=1, 유일한 분할점 k=0
  • 비용 : dp[0][0] + dp[1][1] + 5 * 3 * 2 = 0 + 0 + 30 = 30
  • 따라서 dp[0][1] = 30
• 구간 (1, 2) : $B \times C$
  • i=1, j=2, 유일한 분할점 k=1
  • 비용 : dp[1][1] + dp[2][2] + 3 * 2 * 6 = 0 + 0 + 36 = 36
  • 따라서 dp[1][2] = 36

2. diagonal = 2

• 구간 (0, 2) : $A \times B \times C$
  • i=0, j=2
  • 두 가지 분할 방법이 있음.
    • k=0
      • 왼쪽 : $A$ (비용 0), 오른쪽 : $B \times C$ (비용 dp[1][2] = 36)
      • 곱셈 비용 : 5 * 3 * 6 = 90
      • 총 비용 : 0 + 36 + 90 = 126
    • k=1
      • 왼쪽 : $A \times B$ (비용 dp[0][1] = 30), 오른쪽: $C$ (비용 0)
      • 곱셈 비용 : 5 * 2 * 6 = 60
      • 총 비용 : 30 + 0 + 60 = 90
• 최소 비용으로 90이므로 dp[0][2] = 90

최종적으로, dp[0][n-1] 즉, dp[0][2]에 저장된 값 90이 전체 행렬 곱셈의 최소 연산 횟수가 된다.

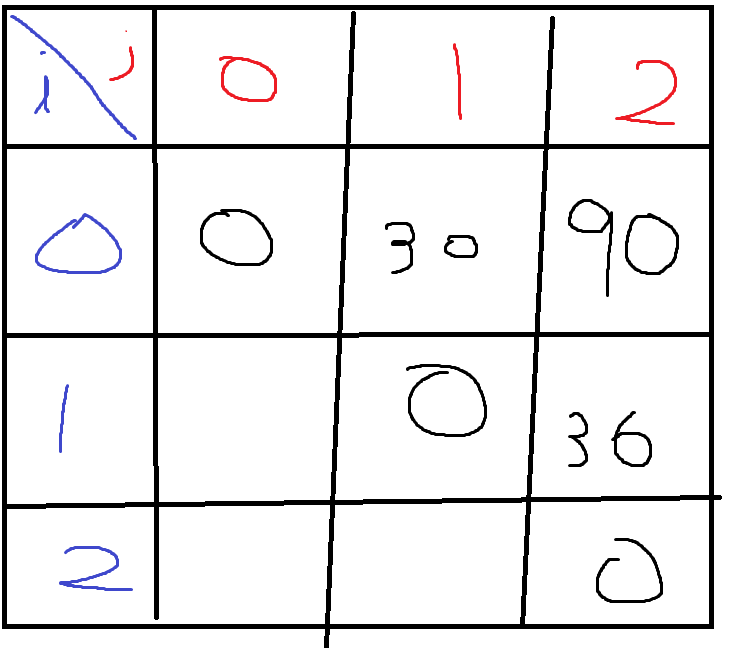
위 과정을 테이블로 그려보면

 

 

1. diagonal = 1

구간 [0, 1] : $A \times B$

가능한 분할은 단 하나 $(k = 0)$ :

$$dp[0][1] = dp[0][0] + dp[1][1] + matrix[0] \times matrix[1] \times matrix[2] = 0 + 0 + 5 \times 3 \times 2 = 30$$

구간 [1, 2] : $B \times C$

가능한 분할은 단 하나 $(k = 1)$ :

$$dp[1][2] = dp[1][1] + dp[2][2] + matrix[1] \times matrix[2] \times matrix[3] = 0 + 0 + 3 \times 2 \times 6 = 36$$

2. diagonal = 2

구간[0, 2] : $A \times B \times C$

• 분할점 k = 0:
• 먼저 $A$와 $(B \times C)$를 계산하는 경우
  $$비용 = dp[0][0] + dp[1][2] + matrix[0] \times matrix[1] \times matrix[3] = 0 + 36 + 5 \times 3 \times  6 = 36 + 90 = 126$$
• 분할점 k = 1 :
  먼저 $(A \times B)$ 와 $C$를 계산하는경우
  $$비용 = dp[0][1] + dp[2][2] + matrix[0] \times matirx[2] \times matrix[3] = 30 + 0 + 5 \times 2 \times 6 = 30 + 60 = 90$$

두 가지 경우 중 최소 비용은 90이므로 

$$dp[0][2] = 90$$