Game of Life
According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."
The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
- Any live cell with fewer than two live neighbors dies as if caused by under-population.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by over-population.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state of the board is determined by applying the above rules simultaneously to every cell in the current state of the m x n grid board. In this process, births and deaths occur simultaneously.
Given the current state of the board, update the board to reflect its next state.
Note that you do not need to return anything.
Example 1:
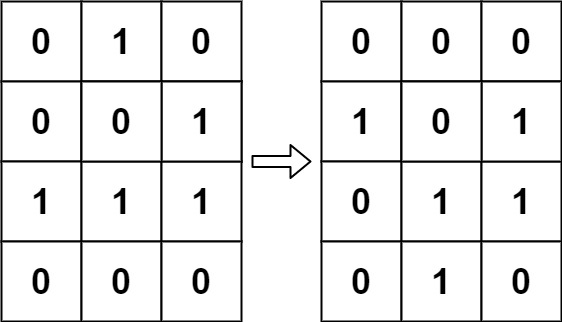
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
Example 2:
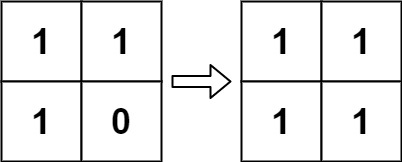
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]
Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 25board[i][j]is0or1.
Follow up:
- Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
- In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
dr = [(-1, 0), (1, 0), (0, -1), (0, 1), (-1, -1), (-1, 1), (1, -1), (1, 1)]
board_copy = copy.deepcopy(board)
n, m = len(board), len(board[0])
for i in range(n) :
for j in range(m) :
cnt = 0
for di, dj in dr :
ni, nj = i + di, j + dj
if 0 <= ni < n and 0 <= nj < m :
cnt += board[ni][nj]
live_or_die = 0
if cnt < 2 and board[i][j] == 1 :
live_or_die = 0
elif 2 <= cnt <= 3 and board[i][j] == 1 :
live_or_die = 1
elif cnt > 3 and board[i][j] == 1 :
live_or_die = 0
elif cnt == 3 and board[i][j] == 0 :
live_or_die = 1
else :
live_or_die = board[i][j]
board_copy[i][j] = live_or_die
for i in range(n) :
for j in range(m) :
board[i][j] = board_copy[i][j]8방향으로 돌아가면서 카운팅을 하고 주어진 조건에 따라 살아남는지 죽는지 정한 다음 복사본에 반영. 이후 원본에 붙여넣기 하면 풀리는 문제.
'알고리즘 스터디' 카테고리의 다른 글
| [Leetcode/파이썬] 35. Search Insert Position (0) | 2025.07.24 |
|---|---|
| [Leetcode/파이썬] 221. Maximal Square (1) | 2025.07.11 |
| [Leetcode/파이썬] 100.Same Tree (0) | 2025.07.10 |
| [Leetcode/파이썬] 114. Flatten Binary Tree to Linked List (0) | 2025.07.03 |
| [Leetcode/파이썬] 13. Roman to Integer (0) | 2025.07.03 |
