[코딩 테스트 합격자 되기 - 12주차] 동적 계획법(Dynamic Programming)

동적 계획법을 간단히 정의하면 전체 문제를 한 번에 해결하는 것이 아니라 작은 부분 문제들을 해결하고, 이것들을 활용하여 전체 문제를 해결하는 방법이라고 할 수 있다. 하지만 부분 문제를 활용하여 전체 문제를 해결했다고 해서 반드시 동적 계획법이 효율적인 것은 아니다. 동적계획법을 효율적으로 활용하려면 아래 두 가지 조건을 만족해야 한다.

 

• 큰 문제를 작은 문제로 나누었을 때 동일한 작은 문제가 반복해서 등장해야 한다.
• 큰 문제의 해결책은 작은 문제의 해결책의 합으로 구성할 수 있어야 한다.

점화식 세우기와 동적 계획법

동적 계획법으로 문제를 해결하는 절차는 다음과 같다.

1. 문제를 해결하는 해가 이미 있다고 가정
2. 종료 조건을 설정
3. 과정 1, 2를 활용하여 점화식을 세움

점화식 구현 : 재귀 활용

점화식을 어떻게 구현할까. 재귀를 활용해보자. 재귀는 재귀 함수의 반환값을 활용한다는 특징이 있다. 

def Fact(N) :
    if N == 1 :
        return 1

    else :
        return Fact(N - 1) * N

 

팩토리얼의 경우, 재귀 방법으로 구현이 가능하다. 

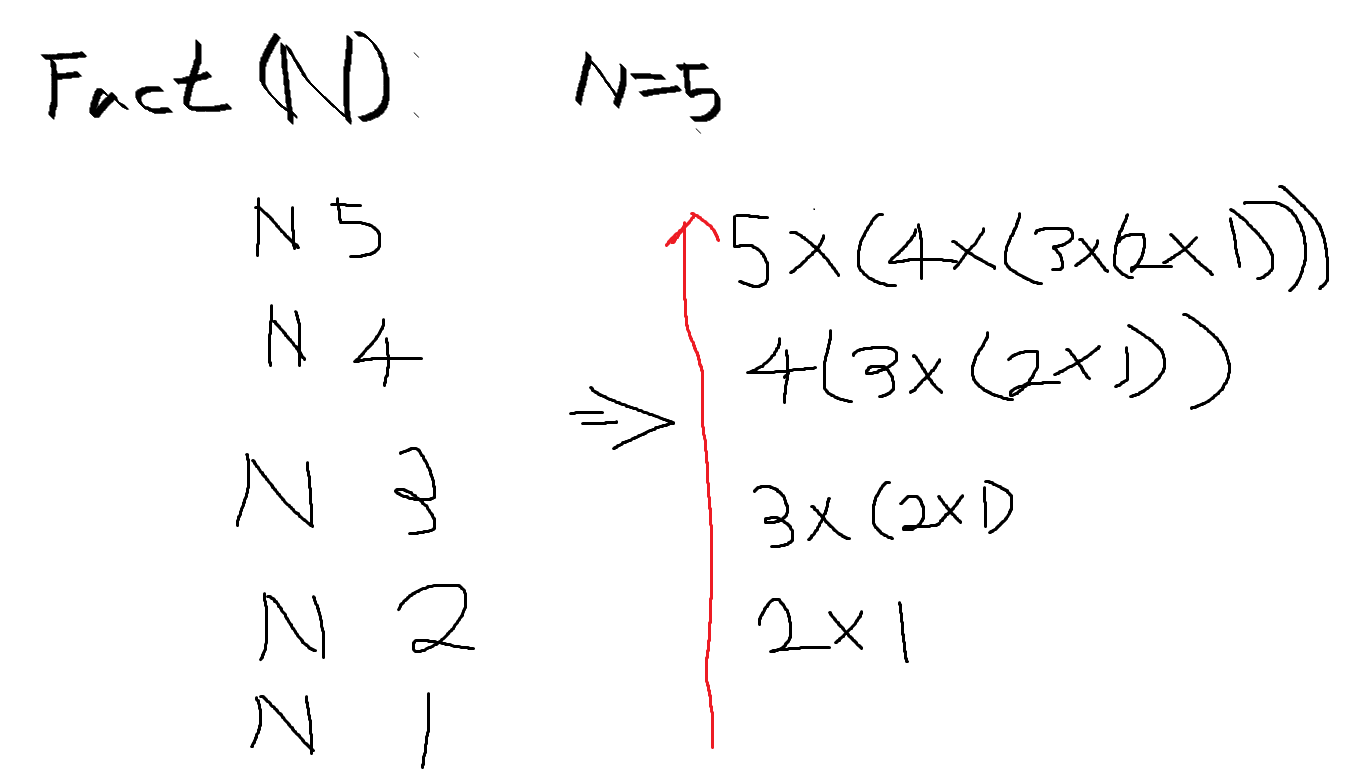
이런 식으로 계산이 될 것이다. 다만 이 방식은 함수를 계속해서 재귀 호출하므로 스택 메모리에 재귀 호출한 함수들이 모두 쌓이는 부담이 있다. 호출한 함수가 많으면 많을수록 스택 메모리에 함수 호출 정보가 많이 쌓일 것이다. 그래서 입력값이 크다면 정답은 맞을지언정 메모리 한계로 런타임 오류가 발생할 수 있다. 그래서 재귀 호출을 사용하기 전에는 항상 메모리 한계에 대한 생각을 하고 이 문제가 발생하지 않도록 하는 것이 중요하다. 재귀 호출 대신 다음의 방법을 활용해보는 것도 좋은 제안이라고 생각한다.

1. 재귀 호출 자체를 쓰지 않는 방법 => 반복문
2. 재귀 호출의 횟수를 줄이는 방법 => 메모이제이션

재귀 호출의 횟수를 줄여주는 메모이제이션

메모이제이션은 이미 계산한 값을 저장해두었다가 이후 쓸 일이 있을 때 활용하는 개념이다. 예를 들어 피보나치 수열을 구현할때, 작은 문제의 해결책의 합으로 큰 문제를 해결할 수 있는 구조이므로, 동적 계획법의 효율을 크게 느낄 수 있는 문제이다.

 

점화식 구현 : 재귀 + 메모이제이션 활용

def fibo(N) :
    if dp[N] != 0 :
        return dp[N]

    if N <= 2:
        dp[N] = 1
    else :
        dp[N] = fibo(N - 1) + fibo(N - 2)

    return dp[N]

N = 10
dp = [0] * (N + 1)
fibo(N)
print(dp)

1. 메모이제이션을 위한 저장소 생성 : 이미 구한 해를 저장할 공간을 생성
2. 재귀 함수 정의 : 점화식을 재귀로 표현할 함수를 정의. 이때 함수의 세부 구현은 고려하지 않는다.
3. 재귀 함수의 종료 조건을 정의 : 피보나치 수의 첫 번째, 두 번째 수는 1로 정해져 있으므로 메모이제이션 저장소에 해를 미리 넣어두고 종료 조건으로 생각.
4. 재귀 함수의 일반 연산 처리 : 보통 동적 계획법에서는 점화식으로 나머지 문제를 처리한다. 그 과정에서 구한 결과값은 메모이제이션에 저장.

대표적인 동적 계획법을 활용하는 문제인 최장 증가 부분 수열(LIS), 최장 공통 부분 수열(LCS)등의 문제를 풀어보면서 동적 계획법에 익숙해져 보자.

 

LeetCode - LIS

 

LeetCode - LCS

 

문제 73 - 피보나치 수

프로그래머스

 

def solution(n) :
    dp = [0] * (n + 1)
    dp[1] = 1
    for i in range(2, n + 1) :
        dp[i] = (dp[i - 1] + dp[i - 2]) % 1234567

    return dp[n]

 

문제 74 - 2 X N 타일링

프로그래머스

 

# 0 = 1 로 놓으면 n을 리턴하면 나올듯
# 1 = 1
# 2 = 2
# 3 = 3
# 4 = 5
# 5 = 8
# 피보나치 인거 같네
def solution(n) :
    dp = [0] * (n + 1)
    dp[0] = dp[1] = 1
    for i in range(2, n + 1) :
        dp[i] = (dp[i - 2] + dp[i - 1]) % 1_000_000_007

    return dp[n]
print(solution(4))

 

문제 75 - 정수 삼각형

프로그래머스

def solution(triangle):
    n = len(triangle)
    dp = [[0] * n for _ in range(n)]
    
    # 배열 가장 아래 라인초기화
    for i in range(n) :
        dp[n-1][i] = triangle[n-1][i]

    # 아래쪽 라인부터 올라가면서 빈 배열 채우기
    for i in range(n - 2, -1, -1) :
        for j in range(i + 1) :
            dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1])+ triangle[i][j]
            
    # 꼭대기 값 리턴
    return dp[0][0]

 

문제 76 - 땅따먹기

프로그래머스

 

def solution(land):
    land_copy = land.copy()
    # 1. 각 행마다 이전 행에서의 최대 점수를 더해가며 최대 점수를 구한다.
    for i in range(1, len(land)) :
        for j in range(4) :
            # 2. 이전 행에서 현재 열의 값을 제외한 나머지 열들 중에서 가장 큰 값을 더해준다.
            # land[i-1][j] 만 빼고 
            land_copy[i][j] += max(land_copy[i-1][:j] + land_copy[i-1][j+1:])

    # 3. 마지막 행에서 얻을 수 있는 최대 점수를 반환한다.
    return max(land_copy[-1])

land[1][j] 에 [2, 3, 5][1, 3, 5][1, 2, 5][1, 2, 3] 중 최고 높은 숫자를 더함.

land[2][j]에 [6, 7, 8][5, 7, 8][5, 6, 8][5, 6, 7] 중 최고 높은 숫자를 더함.

 

[[1, 2, 3, 5], [10, 11, 12, 11], [16, 15, 13, 13]] 이 나옴.

return 하게 되면 16이 나온다. 

핵심은 다음 행에서 같은 열을 제거하는 방법일 것이다. 

land_copy[i][j] += max(land_copy[i-1][:j] + land_copy[i-1][j+1:])

이 코드를 통하여 land[i-1][j]를 제거하고 더하게 되면 문제가 해결된다. 

다른 문제들도 많으니 한 번씩 풀어보길...