99클럽 코테 스터디 6일차 TIL - 그리디

[level 3] 고고학 최고의 발견 - 131702

문제 링크

성능 요약

메모리: 10.2 MB, 시간: 6365.44 ms

구분

코딩테스트 연습 > 연습문제

채점결과

정확성: 100.0
합계: 100.0 / 100.0

제출 일자

2024년 04월 18일 22:21:05

문제 설명

고고학자인 혜선은 오래전부터 성궤의 행방을 추적해왔습니다. 그동안 그의 연구는 주류 학자들로부터 인정받지 못했었지만, 혜선이는 포기하지 않고 조사를 계속했고 마침내 성궤의 행방을 알아내었습니다.

그러나 오래전 누군가로부터 봉인된 성궤는 특별한 잠금장치에 의해 보호되고 있었습니다. 잠금장치는 일종의 퍼즐과 연결되어 퍼즐을 해결하면 열리는 것으로 보입니다.

퍼즐은 시계들이 행렬을 이루는 구조물인데 하나의 시계에 시곗바늘은 하나씩만 있습니다. 각 시곗바늘은 시계방향으로만 돌릴 수 있고 한 번의 조작으로 90도씩 돌릴 수 있습니다. 시계들은 기계장치에 의해 연결되어 있어 어떤 시계의 시곗바늘을 돌리면 그 시계의 상하좌우로 인접한 시계들의 시곗바늘도 함께 돌아갑니다. 행렬의 모서리에 위치한 시계의 시곗바늘을 돌리는 경우에는 인접한 세 시계의 시곗바늘들이 함께 돌아가며, 꼭짓점에 위치한 시계의 시곗바늘을 돌리는 경우에는 인접한 두 시계의 시곗바늘들이 함께 돌아갑니다.

각 시계는 12시, 3시, 6시, 9시 방향 중의 한 방향을 가리키고 있습니다. 각 시계의 시곗바늘을 적절히 조작하여 모든 시곗바늘이 12시 방향을 가리키면 퍼즐이 해결되어 성궤를 봉인하고 있는 잠금장치가 열릴 것입니다.

노후화된 퍼즐 기계장치가 걱정되었던 혜선은 가능한 최소한의 조작으로 퍼즐을 해결하려고 합니다. 시곗바늘들의 행렬 clockHands가 매개변수로 주어질 때, 퍼즐을 해결하기 위한 최소한의 조작 횟수를 return 하도록 solution 함수를 완성해주세요.

---

제한사항

• 2 ≤ clockHands의 길이 ≤ 8
• clockHands는 2차원 배열이며 행과 열의 크기가 동일합니다.
• 0 ≤ clockHands의 원소 ≤ 3
• clockHands[i]의 원소들은 시곗바늘의 방향을 나타내며 0은 12시 방향, 1은 3시 방향, 2는 6시 방향, 3은 9시 방향을 나타냅니다.
• 해결 가능한 퍼즐만 주어집니다.

---

입출력 예

clockHands	result
[[0,3,3,0],[3,2,2,3],[0,3,2,0],[0,3,3,3]]	3

---

입출력 예 설명

입출력 예 #1
2행 2열의 시곗바늘, 2행 3열의 시곗바늘, 4행 3열의 시곗바늘을 각각 한 번씩 돌리면 최소 조작 횟수로 퍼즐을 해결할 수 있습니다.

출처: 프로그래머스 코딩 테스트 연습, https://school.programmers.co.kr/learn/challenges

풀이

import copy

# 상하좌우 및 현재 위치에 대한 변화량
dx = [0, -1, 1, 0, 0]
dy = [0, 0, 0, 1, -1]

# 특정 위치의 시계와 인접한 시계를 회전시키는 함수
def rotate(x, y, lst, rt):
    n = len(lst)  # 시계 배열의 크기
    for k in range(5):  # 현재 위치 및 상하좌우 위치에 대해 반복
        nx, ny = x + dx[k], y + dy[k]
        if 0 <= nx < n and 0 <= ny < n:  # 유효한 위치인지 확인
            lst[ny][nx] = (lst[ny][nx] + rt) % 4  # 시계를 rt만큼 회전

# 최소 회전 횟수를 찾는 함수
def solution(clockHands):
    answer = float('inf')  # 최소 회전 횟수를 저장할 변수, 초기값은 무한대
    n = len(clockHands)  # 시계 배열의 크기

    # 첫 번째 열에 대해 가능한 모든 회전 조합을 시도
    for i in range(4 ** n):
        tmp = 0  # 현재 조합에 대한 회전 횟수
        tmp_clock = copy.deepcopy(clockHands)  # 시계 배열의 복사본 생성
        for j in range(n):  # 첫 번째 열에 대해 반복
            rt = i % 4 ** (j + 1) // 4 ** j  # j번째 시계의 회전 횟수 계산
            if rt == 0:
                continue

            rotate(j, 0, tmp_clock, rt)  # j번째 시계와 인접한 시계들 회전
            tmp += rt  # 회전 횟수 추가

        # 두 번째 열부터 마지막 열까지 현재 조건을 만족하는지 확인하며 회전
        for y in range(1, n):
            for x in range(n):
                if tmp_clock[y - 1][x] == 0:  # 이전 열의 시계가 12시를 가리키면 패스
                    continue
                rt = 4 - tmp_clock[y - 1][x]  # 필요한 회전 횟수 계산
                rotate(x, y, tmp_clock, rt)  # 회전
                tmp += rt  # 회전 횟수 추가

        # 마지막 행이 모두 12시를 가리키는지 확인
        if sum(tmp_clock[-1]) == 0:
            answer = min(answer, tmp)  # 최소 회전 횟수 업데이트

    return answer  # 최소 회전 횟수 반환

그리디 알고리즘.
첫 번째 행부터 차례대로 내려온다면, 첫 번째 행은 두 번째 행에, 두 번째 행은 세 번째 행에, 이런 식으로 n - 1번째 행은 n번째 행의 좌표에 종속적이다. 12시를 가리키지 않는 (i, j)번째 좌표를 12시로 가리키게 하기 위해, (i, j+1)번째 좌표 및 그와 인접한 모든 좌표를 동시에 회전시키면 되며, 이를 각 행에 걸쳐 차례대로 수행한다. 이 모든 작업을 수행하였을 때 마지막 줄의 모든 시계바늘이 12시를 가리키고 있다면 정답이 될 수 있다.

위 알고리즘대로 그리디하게 풀이하게 되면 꽤 오랜 회전을 필요로하며, 정답 여부도 불투명하다. 하지만 우리는 직관적으로 단 1번의 회전만에 이 문제를 해결할 수 있음을 알 수 있다. 이는 위 알고리즘의 회전이 둘째 행에서부터 일어나기 때문이며, 첫 번째 행의 회전 역시 고려해주어야 함을 의미한다. 맨 윗줄을 돌리는 경우의 수는 최대 4^8 = 65536 가지 이다.

팀원 풀이 - 정내혁의 블로그

def solution(clockHands):
    answer = 0
    n = len(clockHands)  # clockHands의 길이 (시계 배열의 크기)
    least = 192  # 최소 회전 횟수를 저장할 변수, 최대값으로 초기화
    for rotate_num in range(4**n):  # 첫 줄을 돌리는 경우의 수(4의 n제곱 가지)
        rotate_cnt = 0  # 회전 횟수
        flag = True  # 모든 시계가 12시를 가리키는지 확인하는 플래그
        rotated = [[0] * n]  # rotated[i+1][j]는 clockHands[i][j] 칸을 몇 번 회전시켰는지. 테두리 바깥은 없는 것으로 간주
        for i in range(n - 1):
            rotated.append([])
            nxt_rotate_num = 0
            for j in range(n):
                r = rotate_num % 4  # rotate_num의 1의 자리가 맨 앞 칸의 회전 횟수
                rotate_cnt += r
                rotate_num //= 4
                rotated[i+1].append(r)
            rotated[i+1].append(0)  # 테두리 바깥을 없는 것으로 처리하기 위해 0을 둘러주기

            for j in range(n):
                # 위에서부터 아래로 내려오므로 ㅗ 모양 4칸이 (i,j) 칸에 이미 영향을 주었고 그 아래 칸이 다음 줄에서 영향을 줄 것
                nxt_rotate_num += (-clockHands[i][j] - sum(rotated[i+1][j-k] for k in range(-1, 2)) - rotated[i][j]) % 4 * 4 ** j
            rotate_num = nxt_rotate_num

        rotated.append([])
        for j in range(n):  # 맨 마지막 줄만 따로 돌려서 그 다음 줄로 맞추는 것이 아니라 flag를 확인
            r = rotate_num % 4
            rotate_cnt += r
            rotate_num //= 4
            rotated[n].append(r)
        rotated[n].append(0)

        for j in range(n):
            # 맨 밑줄에서 틀린 칸이 있으면 배제
            if (clockHands[n-1][j] + sum(rotated[n][j-k] for k in range(-1, 2)) + rotated[n-1][j]) % 4:
                flag = False
                break
        if flag and rotate_cnt < least:  # 모든 시계가 12시를 가리키고, 현재 최소 회전 횟수보다 작으면 업데이트
            least = rotate_cnt

    answer = least
    return answer

풀이 접근

맨 윗줄의 모든 칸(최대 8칸)을 몇 번씩 돌릴 지(경우의 수 최대 65536) 확정지으면 그 아래 칸들은 전부 확정된다.

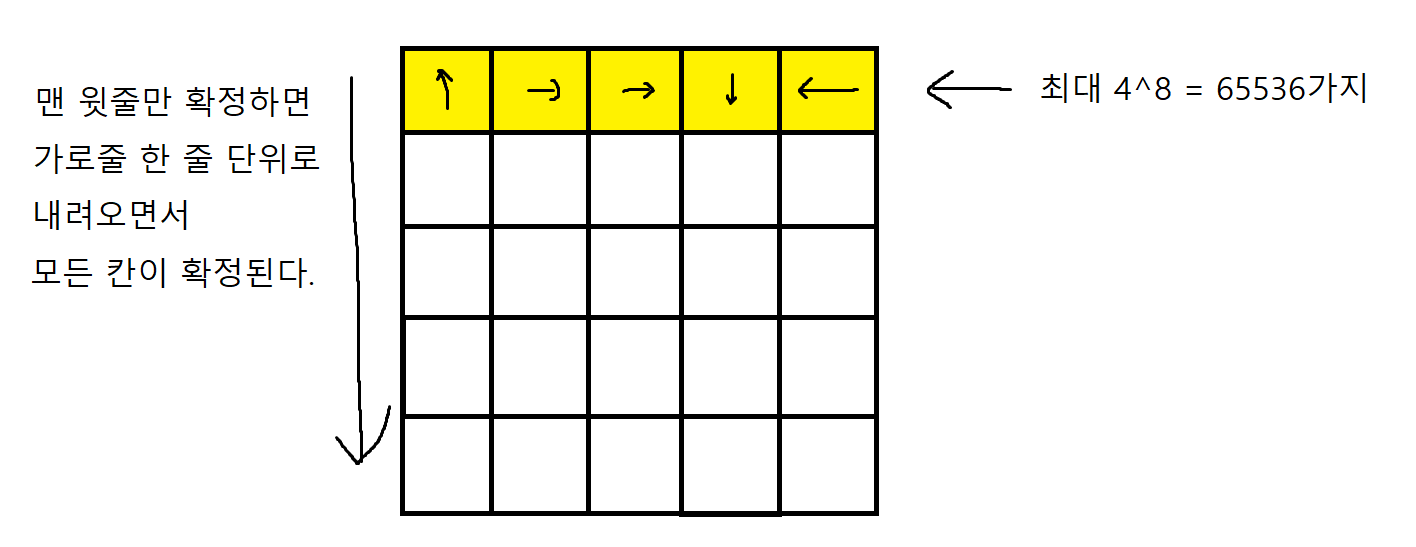
맨 윗줄을 돌리는 경우의 수는 최대 4^8 = 65536가지이다. 이를 픽스해 두면, 맨 윗줄의 각 칸들의 최종적인 상태는 그 아랫칸이 유일하게 결정하게 된다.

따라서 맨 윗줄의 각 칸의 화살표가 12시를 향하도록 그 아랫줄의 각 칸들을 결정하게 되고, 그러고 나면 3번째 줄을 유일하게 결정해서 2번째 줄이 다 12시를 향하도록 해야 하고 ... 맨 밑줄까지 반복할 수 있다.

맨 밑 줄은 그 아랫줄이 없으므로, 유일하게 결정되고 나면 맨 밑줄의 모든 칸이 12시를 향하는지 확인하고, 만약 그렇다면 solve에 성공한 것이므로 총 회전 횟수가 최소였는지만 체크해서 갱신하면 된다.