Search a 2D Matrix
You are given an m x n integer matrix matrix with the following two properties:
- Each row is sorted in non-decreasing order.
- The first integer of each row is greater than the last integer of the previous row.
Given an integer target, return true if target is in matrix or false otherwise.
You must write a solution in O(log(m * n)) time complexity.
Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true
Example 2:
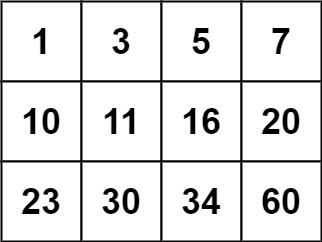
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
left, right = 0, len(matrix)-1
while left <= right :
mid = (left + right) // 2
if matrix[mid][0] <= target <= matrix[mid][-1] :
break
elif target > matrix[mid][0] :
left += 1
else :
right -= 1
lst = matrix[mid]
left, right = 0, len(lst) - 1
while left <= right :
mid = (left + right) // 2
if target == lst[mid] :
return True
elif target > lst[mid] :
left += 1
else :
right -= 1
return Falseclass Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
for i in range(len(matrix)) :
mn, mx = matrix[i][0], matrix[i][-1]
if mn < target < mx :
left, right = 0, len(matrix[0]) - 1
while left <= right :
mid = (left + right) // 2
if target == matrix[i][mid] :
return True
elif target > matrix[i][mid] :
left += 1
else :
right -= 1
elif mn == target or mx == target:
return True
else :
continue
return False문제 풀이는 2개이다. 내가 직접 생각했던 풀이는 두번째 풀이이며, 문제에서 요구하는대로 풀게되면 첫번째 풀이가 옳게 된다.
문제의 가장 마지막 부분을 보면 $O(log(m*n))$ 으로 풀어라고 되어있다. 이는 로그법칙에 의해서 $O(logN + logM)$ 으로 풀어라는 소리이다. 언제나 시간복잡도에서 $log$를 보게 되면 가장 먼저 떠오르는 풀이 방법은 이분탐색 방법이다. 문제의 의도대로 이분탐색을 2번 사용하게 되면 이 문제에서 요구하는 대로 문제를 풀게 되는 것이라고 생각한다. 그래서 첫번째 풀이로 풀어보려고 했지만 도저히 생각이 안나더라...
내가 했던 두번째 풀이 방법도 크게 다르진 않지만 개인적으로는 더 쉽게 느껴졌다. 하나의 블록으로 되어 있어서 그런가 싶기도 하다.
for loop로 가장 matrix 의 가장 윗부분 부터 아랫부분까지 순차적으로 돌면서 일을 진행한다. 그 중 가장 앞부분을 min, 가장 뒷부분을 max 변수에 넣고 이분탐색을 시작한다.
파이썬의 장점을 활용하여 target 을 가운데로 두고 min, max 에 해당하는 변수들과 비교한다. 이 사이에 있으면 이분탐색을 실시한다.
이 후 for문을 다 돌게되었음에도 True를 반환하지 않으면 False를 반환한다.
이 글을 작성하면서 if 문들의 순서를 바꾸는것이 더 좋으려나 이런 생각도 해보게 된다. 일단 통과되었으니까 상관 없겠지..?
이 문제를 자세하게 보면 이분탐색을 2번 사용하여 문제를 해결하는 것을 보고 싶어서 문제를 낸 듯 싶었다.
'알고리즘 스터디' 카테고리의 다른 글
| [Leetcode/파이썬] 117. Populating Next Right Pointers in Each Node II (0) | 2025.11.12 |
|---|---|
| [Leetcode/파이썬] 120. Triangle (0) | 2025.11.09 |
| [Leetcode/파이썬] 46. Permutations (0) | 2025.10.31 |
| [Leetcode/파이썬] 130. Surrounded Regions (0) | 2025.10.31 |
| [Leetcode/파이썬] 61. Rotate List (0) | 2025.10.30 |
