[코딩 테스트 합격자 되기 - 13주차] 그리디(Greedy)

탐욕 알고리즘, 그리디 알고리즘 등으로 불리우는 탐욕법, 그리디...

그리디 알고리즘은 문제 해결 과정에서 결정 순간마다 눈 앞에 보이는 최선의 선택을 하며 선택을 번복하지 않습니다.

이런 특성으로 '그리디 알고리즘은 지역 최적해를 추구한다' 라고 말하기도 합니다. 부분적으로는 최적해를 구한다고 할 순 있어도 전체적으로 최선의 해를 구했는가에 대해서는 확실한 상황은 아니다.

그리디 알고리즘으로 거스름돈 내어주기

손님에게 8원을 거슬러 줘야 하는데 동전 종류가 5, 4, 1원만 있는 상황이라면, 동전 개수가 가장 적게 만드는 알고리즘을 적용하였을 때의 답은 무엇일까?

1. 값이 가장 큰 동전부터 주는 방법이 있다. 그리디 알고리즘은 현재 상황에서 최선의 선택을 하니 값이 가장 큰 동전부터 준다고 생각한다는 것이다. 그러니 5원부터 생각합니다. 5원을 주면 3원을 거스름돈으로 더 주면 된다.
2. 나머지 3원은 1원 3개를 주는 방법 밖에 없다. 동전의 개수는 총 4개 가 된다.
3. 그러나 우리는 4원 2개를 주는 해가 가장 최적의 해라는 것을 알 수 있다. 하지만 그리디 알고리즘은 8원을 줘야하는 상황에서 가장 큰 값의 동전을 고를 수 밖에 없다. 그래서 그리디 알고리즘이 항상 최적의 해를 보장하진 못한다.

그리디 알고리즘이 최적해를 보장하려면?

하지만 그리디 알고리즘은 특정한 상황에서 최적해를 보장하므로 이를 활용하면 문제를 잘 해결할 수 있습니다.

• 최적 부분 구조 : 부분해를 푸는 과정이 최적해를 구하는 과정과 일치
• 그리디 선택 속성 : 선택 과정이 다른 과정에 영향을 주지 않음

그리디 알고리즘이 최적 부분 구조에 어긋나는 이유는 부분해를 푸는 것이 전체 해를 푸는 데에 도움을 주지 않는다는 것이다. 방금 거스름돈 문제에서 8원을 거스름돈으로 주는 상황에서 5원 동전을 먼저 선택하면 그 다음에는 4원 동전을 선택할 수 없습니다. 5원 동전을 먼저 선택한 것이 제약이 되어 동전 개수를 최소로 할 수 없게 된다. 이렇게 그리디한 선택은 선택에 제약을 주며 최적의 해를 구하지 못하기도 한다. 5원을 거슬러 주는 선택은 이후 거스름돈을 주는 선택에 영향을 준다.

이런 그리디 알고리즘의 특징은 항상 최적해를 도출하지 못한다는 한계를 보여준다. 그러나 그리디 알고리즘이 무용지물은 아니다. 그리디 알고리즘은 빠른 시간 내에 근사해를 제공하는 효율적인 방법 중 하나이므로 문제의 특성과 알고리즘 선택 기준을 잘 이해했다면 매우 유용한 알고리즘이라고 할 수 있다.

최소 신장 트리(Mininum Spanning Tree, MST)

최소 신장 트리는 그리디 알고리즘을 사용하는 태표적인 트리 형태의 자료구조이다.

 

신장트리는 모든 정점이 간선으로 연결되어 있고 간선 개수가 정점 개수보다 하나 적은 그래프를 말한다.

위키 백과 - 신장 부분 그래프

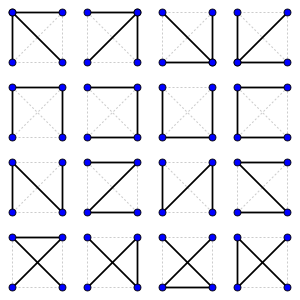
최소 신장 트리는 신장 트리 중 간선의 가중치 합이 최소면 최소 신장트리라고 한다. 경우에 따라 최소 신장 트리는 하나가 아닐 수도 있다. 

최소 신장 트리의 경우, 대표적으로 항공기의 운항 경로나 네트워크 분야에서도 많이 사용된다.

 

최소 신장 트리를 구하는 그리디 알고리즘

최소 신장 트리를 구하는 대표적인 그리디 알고리즘은 프림 알고리즘과 크루스칼 알고리즘 이다.

 

배낭 문제 (Knapsack problem)

배낭 문제라는 아주 유명한 문제가 존재한다. 배낭에 담을 수 있는 최대 무게가 존재하고, 무게와 가치가 다른 짐들이 있다. 이 짐들을 잘 조합해서 배낭의 무게를 초과하지 않으면서 담은 가치를 최대로 하는 문제를 배낭 문제라고 한다. 배낭문제는 대체로 쪼갤 수 있는지 없는지에 따라 부분 배낭 문제 또는 0-1 배낭 문제로 나뉘게 된다. 

 

부분 배낭 문제(Fractional Knapsack Problem)

부분 배낭 문제를 해결하려면, 무게당 가치가 높은 짐을 최대한 많이 넣는 그리디 알고리즘을 사용해야 한다. 

1. 짐 별로 무게당 가치를 구한다.
2. 무게당 가치가 높은 짐부터 넣을 수 있는 만큼 배낭에 넣는다.
   1. 배낭 용량이 짐 무게보다 크면 짐을 쪼개서 넣는다.
3. 과정 2를 배낭이 허용하는 용량이 0이 될 때까지 수행한다.

이렇게 그리디 알고리즘으로 부분 배낭 문제를 풀 수 있다. 실제로 매 순간 짐을 선택하는 방식은 무게당 가치가 높은 짐이므로 최적 부분 구조를 만족한다. 그리고 짐을 쪼갤 수 있으니 앞에서 선택한 짐이 다른 짐 선택에 영향을 주지도 않으므로 탐욕적 선택 요소에도 만족한다. 따라서 이 방식은 최적해를 보장한다고 할 수 있다. 

 

0-1 배낭 문제(0-1 Knapsack Problem)

이 문제는 짐을 쪼갤 수 없으므로 지금 선택한 짐이 다음 짐 선택에 영향을 준다. 그래서 그리디 알고리즘을 적용하면 최적의 해를 구할 수 없다. 최적의 해를 구하려면 동적 계획법으로 접근해야 한다.