99클럽 코테 스터디 14일차 TIL - 백준 3976 역습 - 동적 계획법

[Silver II] 역습 - 3976

문제 링크

성능 요약

메모리: 192424 KB, 시간: 440 ms

분류

다이나믹 프로그래밍

제출 일자

2024년 4월 25일 01:54:42

문제 설명

축구에서 역습은 매우 중요한 전술이다. WeissBlume FC는 수비 할 때, 스트라이커 두명을 제외하고는 모두 자기 진영에서 수비를 한다. 이때, 수비수가 상대방의 공을 따게 되면, 스트라이커에게 긴 패스를 하면서 역습을 시작한다. 두 스트라이커는 모두 서로가 어떻게 움직일지 알고 있고, 어떤 점에서는 다른 스트라이커에게 공을 패스할 수도 있다.

이러한 상황에서 역습을 전개해가는 과정은 매우 다양하게 전개될 수 있다. 먼저, 수비수는 어떤 스트라이커에게 공을 연결해야 할지 결정을 해야 하고, 공을 소유하고 있는 스트라이커는 공을 드리블할지, 패스를 해야할지, 슛을 해야할지 결정을 해야 한다. 이런 4가지 행동(긴 패스, 드리블, 패스, 슛)은 실패할 수도 있다. 따라서, 감독은 이 모든 행동에 난이도를 계산했다.

WeissBlume FC가 이상적으로 경기를 진행할 때, 최소 난이도를 구하는 프로그램을 작성하시오.

위의 그림에서 수비는 왼쪽 진영의 X마크이다. 이때, 오른쪽 진영의 X는 스트라이커이다. 스트라이커는 미리 정해진 경로를 동시에 움직인다. 미리 지정해논 점(원)에서는 공을 드리블 해서 다음 점으로 이동할지, 다른 스트라이커에게 패스를 할 지 결정을 해야 한다. 마지막 점에서 스트라이커는 슛을 하면 된다.

입력

첫째 줄에 테스트 케이스의 개수 c가 주어진다. (1 ≤ c ≤ 100) 각각의 테스트 케이스는 다섯 줄로 이루어져 있다.

테스트 케이스의 첫째 줄에는 각 스트라이커가 이동하는 방법에서 미리 지정해논 점의 개수 n이 주어진다. (2 ≤ n ≤ 100,000) n 다음에는 l1, l2, s1, s2이 주어진다. l1과 l2은 수비수가 스트라이커에게 긴 패스를 할 때 난이도이고, s1과 s2은 스트라이커가 슛을 할 때의 난이도이다.

그 다음 줄에는 첫 번째 스트라이커가 i번 점에서 두 번째 스트라이커의 i+1번 점으로 패스를 할 때의 난이도 n-1개가 주어진다. 다음 줄에는 첫 번째 스트라이커가 i번 점에서 i + 1 드리블 할 때의 난이도 n-1개가 주어진다.

그 다음 줄에는 두 번째 스트라이커가 i번 점에서 첫 번째 스트라이커의 i+1번 점으로 패스를 할 때의 난이도 n-1개가 주어진다. 다음 줄에는 두 번째 스트라이커가 i번 점에서 i + 1 드리블 할 때의 난이도 n-1개가 주어진다.

모든 난이도는 1000보다 작거나 같은 음이 아닌 정수이다.

출력

각각의 테스트 케이스에 대해서, 골로 연결하는데 필요한 난이도의 최솟값을 출력한다.

 

풀이

T = int(input())
for _ in range(T) :
    n, l1, l2, s1, s2 = map(int, input().split())   # 점, 수비수가 스트라이커한테 긴패스1, 2, 스트라이커 슛 1, 2
    p1 = list(map(int, input().split()))            # 스트라이커1 => 2 패스 난이도
    d1 = list(map(int, input().split()))            # 스트라이커1 드리블
    p2 = list(map(int, input().split()))            # 스트라이커2 => 1 패스 난이도
    d2 = list(map(int, input().split()))            # 스트라이커2 드리블

    dp = [[0] * 2 for _ in range(n+1)]              # [0] = 1번 루트, [1] = 2번 루트

    # 첫 번째 점에서의 난이도 초기화
    dp[1][0] = l1
    dp[1][1] = l2

    # 각 점에서의 최소 난이도 계산
    for i in range(2, n+1) :
        # l1 => d1 or p2
        dp[i][0] = min(dp[i-1][0] + d1[i-2], dp[i-1][1] + p2[i-2])
        # l2 => d2 or p1
        dp[i][1] = min(dp[i-1][1] + d2[i-2], dp[i-1][0] + p1[i-2])

    ans = min(dp[n][0] + s1, dp[n][1] + s2)
    print(ans)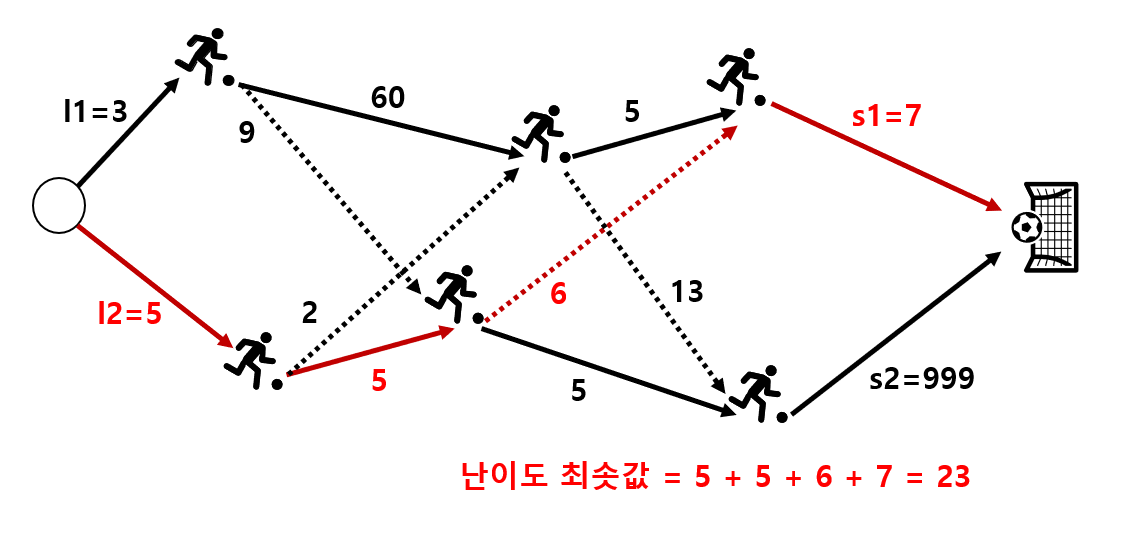

참고한 블로그

[C/C++] 백준 3976번 - 역습 (DP)

 

그림으로 설명한 블로그 중 가장 잘 설명한 것 같아서 가져왔다. 결국 그래프를 지나면서 결국 최소값을 가지는 알고리즘을 작성하였다. 

동적 계획법을 사용해 최소값을 찾아가면서 진행하였다. 

1번에서 드리블로 1번으로 쭉 가는지, 2번으로 패스하는지 혹은 2번에서 드리블로 2번으로 쭉 가는지, 1번으로 패스하는지, 이 두가지 사항을 반복문을 통해서 비교하여 최소값을 dp 배열에 담아준다. 그래서 dp 배열을 2차원 배열로 만들어 처리하였다. 

 

이번 문제를 공부하면서 동적 계획법에 대해서 조금 더 공부할 수 있는 시간이었다. 동적 계획법 + 구현만 잘 해낸다면 크게 어려운 문제는 아니라고 생각한다.