그래프는 노드(vertex)와 간선(edge)을 이용한 비선형 데이터 구조 . 보통 그래프는 데이터 간의 관계를 표현하는 데 사용됨. 데이터를 노드로, 노드 간의 관계나 흐름을 간선으로 표현함. 간선은 방향이 있을 수도, 없을 수도 있음. 만약 관계나 흐름에서 정도를 표현할 필요가 있다면 가중치라는 개념을 추가하여 표현하기도 함.
그래프 용어 정리
예를 들어 도시 간의 인구 이동을 그래프로 표현하면 다음과 같다.

그림에서 사각형으로 표현한 것은 노드(또는 정점), 화살표로 표현한 것은 간선, 간선 위에 숫자로 표현한 것은 가중치다. 노드에는 어떤 데이터가 들어있다. 인구 이동의 경우 어디서 얼마나 이동했는지 표시할 필요가 있으므로 간선에 가중치를 표현함.
흐름을 표현하는 방향성
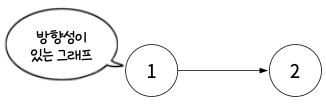
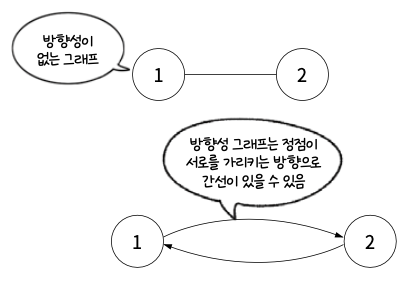
간선은 방향을 가질 수도 있고 없을 수도 있음.
- 방향 그래프 : 방향이 있는 간선을 포함함
- 무방향 그래프 : 방향이 없는 간선을 포함함.
이때 방향 그래프는 어느 한쪽으로만 방향이 있는 간선이 있는 것이 아니라 서로 반대를 가리키는 간선이 있을 수도 있다.
흐름의 정도를 표현하는 가중치
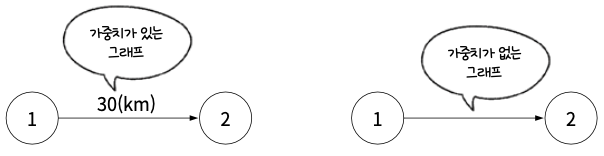
어떤 데이터는 흐름의 방향 뿐 아니라 양도 중요할 수 있음. 그런 정도를 간선에 표현할 때 이를 가중치라 함. 가중치가 있는 그래프를 가중치 그래프라고 함.
시작과 끝의 연결 여부를 보는 순환
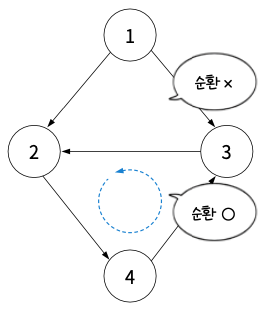
순환은 특정 노드에서 시작해 간선을 따라 다시 돌아오는 경로가 있는 것을 의미함. 순환이 존재하는 그래프를 순환 그래프라 하고, 순환이 존재하지 않는 그래프를 비순환 그래프라고 함.

특정 노드에서 시작해 간선을 따라 다시 돌아오면 순환 그래프.
그래프 구현
예를 들어 서울에서 부산으로 유동 인구 8,000명이 발생했다와 같은 내용을 그래프로 표현한다면, 그래프의 노드, 간선, 방향, 가중치와 문장의 의미를 이렇게 연결하여 정리할 수 있음.
- 데이터를 담고 있는 노드(서울, 부산)
- 노드를 잇는 간선(서울과 부산의 연결 유무)
- 간선의 방향(서울에서 부산 방향으로)
- 간선의 가중치(유동 인구 8,000명)
그래프의 구현 방식에는 인접 행렬(Adjacency Matrix)과 인접 리스트(Adjacency List)가 있음.
인접 행렬 그래프 표현
인접 행렬은 배열을 활용하여 구현하는 경우가 많음. 이때 배열의 인덱스는 노드, 배열의 값은 노드의 가중치로 생각하고, 인덱스의 세로 방향을 출발 노드, 가로 방향을 도착 노드로 생각하면 자연스럽게 그래프를 표현할 수 있으며, 이를 인접 행렬로 표현하면 다음과 같다.

인접 행렬의 세로 방향 인덱스를 출발, 가로 방향 인덱스를 도착으로 하니 서울(0) -> 부산(1)으로 향하는 가중치 400(km)인 그래프가를 표현함. - 로 표현된 가중치는 실제 코드에서는 굉장히 큰 값을 넣거나 -1로 정함.
인접 리스트 그래프 표현
인접 리스트로 그래프를 표현하려면 정점(v), 가중치(w), 다음 노드(next)를 묶어서 관리함.
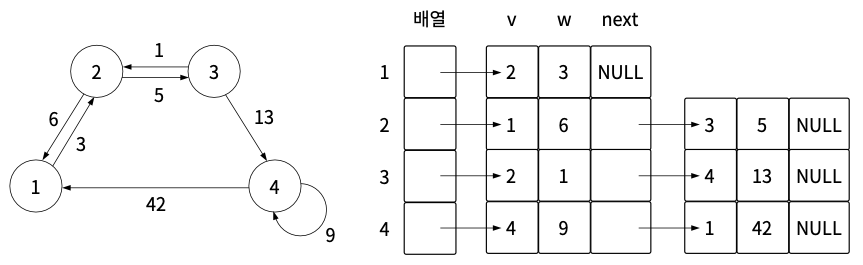
인접 행렬과 인접 리스트로 표현한 그래프는 다음과 같은 장단점을 갖는다.
| 메모리 사용 | 시간 복잡도 | 기타 | |
| 인접 행렬 | O(N^2) | O(1) | 구현이 상대적으로 쉬움 |
| 인접 리스트 | O(N + M) | O(N) |
그래프 문제를 풀 때는 인접 행렬과 인접 리스트 방식 중 더 좋은 것을 선택해야 하지만 보통 시간 제약에서 장점을 취하기 위해서는 인접 행렬 방식으로 그래프 문제를 푸는 경우가 많다. 문제에서 노드 개수가 1,000개 미만으로 주어지는 경우에 인접 행렬을 사용하면 됨.
그래프 탐색
- 깊이 우선 탐색(DFS) : 더 이상 탐색할 노드가 없을 때까지 일단 간 다음, 더 이상 탐색할 노드가 없으면 최근에 방문했던 노드로 돌아가 다음 가지 않은 노드를 방문함.
- 너비 우선 탐색(BFS) : 현재 위치에서 가장 가까운 노드부터 모두 방문하고 다음 노드로 넘어감. 그 노드에서 또 다시 가장 가까운 노드부터 모두 방문함.
깊이 우선 탐색 (DFS)
이 탐색은 주로 스택을 활용함. 탐색을 하려면 일단 시작 노드를 정하고, 스택에 시작 노드를 푸시함. 스택에 있는 노드는 아직 방문하지 않았지만 방문할 예정인 노드. 시작 노드를 푸시했으면 다음 과정을 반복
- 스택이 비어있는지 확인. 스택이 비어있으면 방문할 수 있는 모든 노드를 방문했음을 의미함. 따라서 스택이 비었으면 탐색을 종료
- 스택에서 노드를 팝.
- 팝한 노드의 방문 여부를 확인. 아직 방문하지 않았다면 노드를 방문 처리함
- 방문한 노드와 인접한 모든 노드를 확인. 그리고 그 중에서 아직 방문하지 않은 노드를 스택에 푸시. 스택은 FILO(First In Last Out) 구조이므로 방문 순서를 오름차순으로 고려한다면 역순으로 노드를 푸시해야 함.
고려사항
- 탐색할 노드가 없을 때까지 간선을 타고 내려갈 수 있어야 함.
- 가장 최근에 방문한 노드를 알아야 함.
- 이미 방문한 노드인지 확인 가능해야 함.
'가장 깊은 노드까지 방문한 후에 더 이상 방문할 노드가 없으면 최근 방문한 노드로 돌아온 다음, 해당 노드에 방문할 노드가 있는지 확인.'

백트래킹(Back Tracking). 탐색하고 있는 방향의 역방향으로 돌아가는 동작.
스택은 최근에 푸시한 노드를 팝할 수 있으므로 특정 노드를 방문하기 전에 최근 방문 노드를 팝 연산으로 쉽게 확인할 수 있음. 이런 스택의 특성을 활용해 백트래킹 동작을 쉽게 구현 가능.
재귀를 활용한 깊이 우선 탐색
해당 도서에는 스택과 재귀를 활용한 깊이 우선 탐색을 제시하고 있음. 그러나 본 글에는 재귀를 활용한 깊이 우선 탐색만 작성함. 자세한 설명이나 추가 내용은 책이나 골든래빗 컬럼을 참고.
재귀 함수를 호출할 때마다 호출한 함수는 시스템 스택이라는 곳에 쌓이므로 깊이 우선 탐색에 활용 가능함. 호출할 함수는 dfs()라 선언하고 dfs(N)을 호출하면 다음 동작을 하도록 구현했다고 가정한다면,
- dfs(N) : N번 노드를 방문 처리하고 N번 노드와 인접한 노드 중 아직 방문하지 않은 노드를 탐색
- 시작 노드는 1번 노드이므로 dfs(1)을 호출. dfs(1)이 실행되면 1을 방문 처리하고 내부적으로 dfs(4)를 재귀 호출. 아직 dfs(1)은 dfs(4)를 호출한 상태이므로 종료되지 않았음. 따라서 스택에 dfs(1)이 쌓임.

- dfs(4)가 실행되므로 4는 방문 처리하며, 내부적으로 dfs(4)는 dfs(2)를 호출함.

- dfs(2)를 실행. 2를 방문 처리하고 dfs(2)는 dfs(3)을 재귀 호출
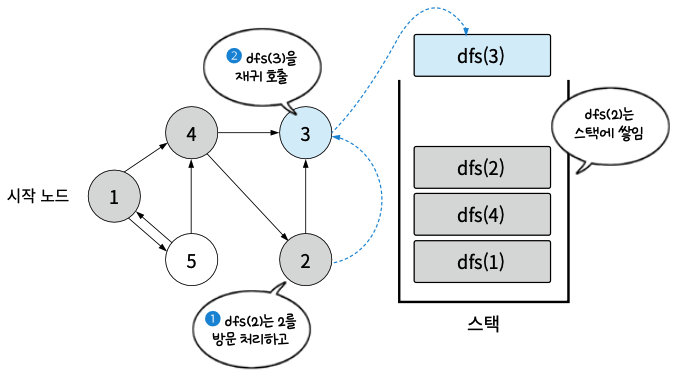
- dfs(3)을 실행. 3은 인접 노드가 없으므로 추가 재귀 호출을 하지 않고 함수를 종료.

- 스택 특성에 의해 dfs(2)로 돌아가 다음 실행 스텝을 진행. 그러나 2는 인접 노드가 없으므로 종료

- dfs(4)로 돌아가 다음 실행 스텝을 진행. 4도 인접 노드가 없음. 함수 종료
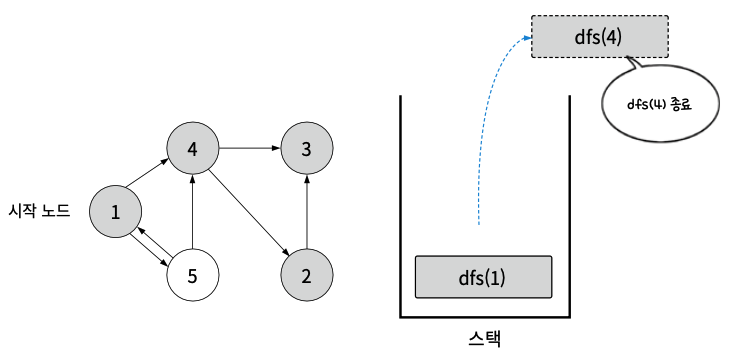
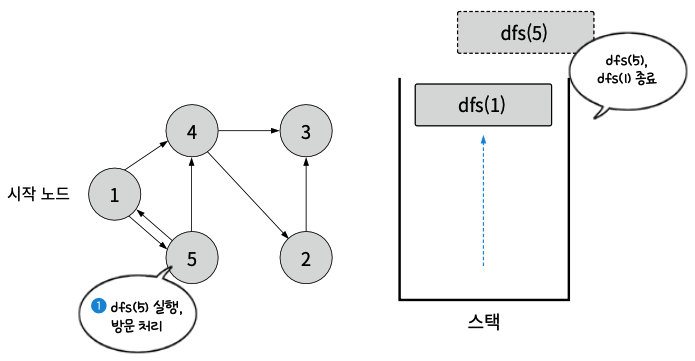
- dfs(1)의 다음 실행 스텝을 진행. dfs(5) 호출
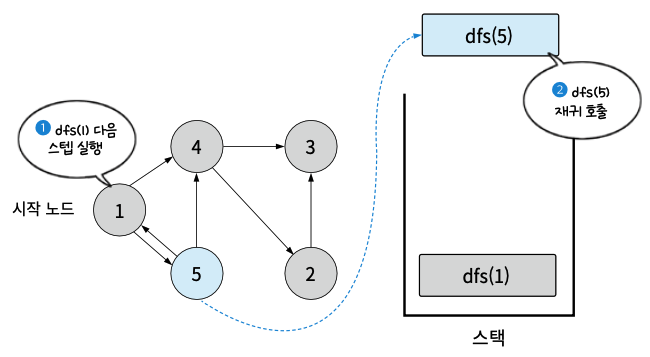
- dfs(5)를 실행. 5를 방문 처리하고 5와 인접한 노드가 없으므로 dfs(5) 종료. 이어 dfs(1) 종료
너비 우선 탐색(BFS)
너비 우선 탐색은 시작 노드와 거리가 가장 가까운 노드를 우선하여 방문하는 방식의 알고리즘. 여기서의 거리는 시작 노드와 목표 노드까지의 차수. 탐색을 하려면 일단 시작 노드를 정하고, 큐에 시작 노드를 푸시. 시작 노드를 큐에 푸시하면서 방문 처리. 큐에 있는 노드는 이미 방문 처리했고, 그 노드와 인접한 노드는 아직 탐색하지 않은 상태. 이후 다음 과정을 반복함.
- 큐가 비었는지 확인. 큐가 비었다면 방문할 수 있는 모든 노드를 방문했다는 의미(탐색 종료).
- 큐에 노드를 팝
- 팝한 노드와 인접한 모든 노드를 확인하고 그 중 아직 방문하지 않은 노드를 큐에 푸시하며 방문 처리함.
고려사항
- 현재 방문한 노드와 직접 연결된 모든 노드를 방문할 수 있어야 함.
- 이미 방문한 노드인지 확인할 수 있어야 함.
너비 우선 탐색을 보면 시작 노드 부터 인접한 노드를 모두 방문한 후 그 다음 단계의 인접 노드를 방문함. 즉, 먼저 발견한 노드를 방문. 이러한 특성 때문에 너비 우선 탐색을 할 때는 큐를 활용함.
큐를 활용한 너비 우선 탐색
- 시작 노드 1을 큐에 푸시하고 방문 처리

- 1을 팝한 후 인접한 4와 5를 방문 처리하고 4, 5 순서로 큐에 푸시
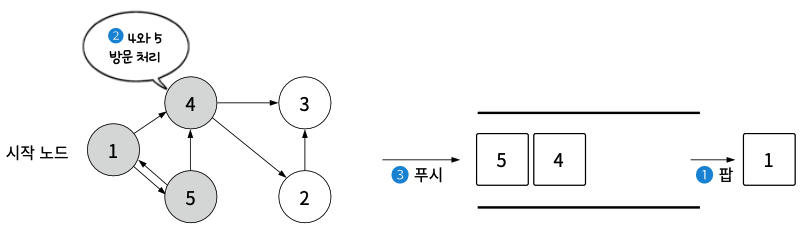
- 4를 팝한 후 인접한 2와 3을 방문 처리하고 2, 3 순서로 큐에 푸시
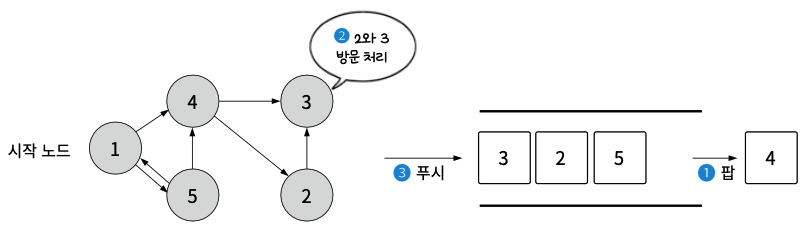
- 5를 팝한 후 인접한 1과 4, 이 두 노드는 이미 방문 했으므로 아무것도 하지않고 팝만 함.
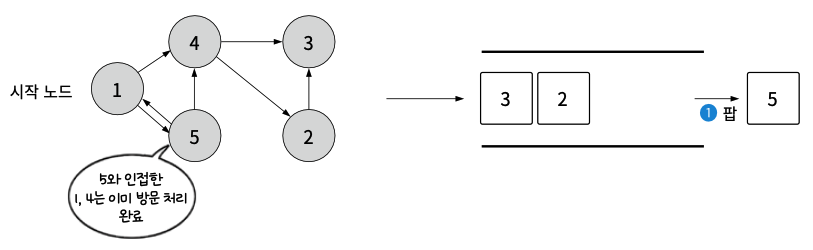
- 이후 나머지 노드들도 모두 방문하였으므로 팝.

깊이 우선 탐색과 너비 우선 탐색 비교
- 깊이 탐색 후 되돌아오는 깊이 우선 탐색
가장 깊은 곳을 우선하여 탐색하고, 더 이상 탐색할 수 없으면 백트래킹하여 최근 방문 노드부터 다시 탐색을 진행한다는 특징이 있어서 모든 가능한 해를 찾는 백트래킹 알고리즘을 구현할 때나 그래프의 사이클을 감지해야하는 경우 활용할 수 있음.
코딩 테스트에서는 탐색을 해야할 때, 최단 경로를 찾는 문제가 아니면 깊이 우선 탐색을 우선 고려하는 것도 좋음. - 최단 경로를 보장하는 너비 우선 탐색
너비 우선 탐색은 찾은 노드가 시작노드로부터 최단 경로임을 보장함. 왜냐하면 시작 노드로부터 직접 간선으로 연결된 모든 노드를 먼저 방문하기 때문. 쉽게 말해, 문제에 대한 답이 많은 경우 너비 우선 탐색은 이 답 중 가장 가까운 답을 찾을 때 유용함. 그래서 미로 찾기 문제에서 최단 경로를 찾거나, 네트워크 분석 문제를 풀 때 너비 우선 탐색을 활용할 수 있음.