[백준/파이썬][Gold II] 트리의 지름 - 1167

[Gold II] 트리의 지름 - 1167

문제 링크

성능 요약

메모리: 146100 KB, 시간: 280 ms

분류

깊이 우선 탐색, 그래프 이론, 그래프 탐색, 트리

제출 일자

2024년 9월 3일 18:48:46

문제 설명

트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.

입력

트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지 매겨져 있다.

먼저 정점 번호가 주어지고, 이어서 연결된 간선의 정보를 의미하는 정수가 두 개씩 주어지는데, 하나는 정점번호, 다른 하나는 그 정점까지의 거리이다. 예를 들어 네 번째 줄의 경우 정점 3은 정점 1과 거리가 2인 간선으로 연결되어 있고, 정점 4와는 거리가 3인 간선으로 연결되어 있는 것을 보여준다. 각 줄의 마지막에는 -1이 입력으로 주어진다. 주어지는 거리는 모두 10,000 이하의 자연수이다.

출력

첫째 줄에 트리의 지름을 출력한다.

풀이

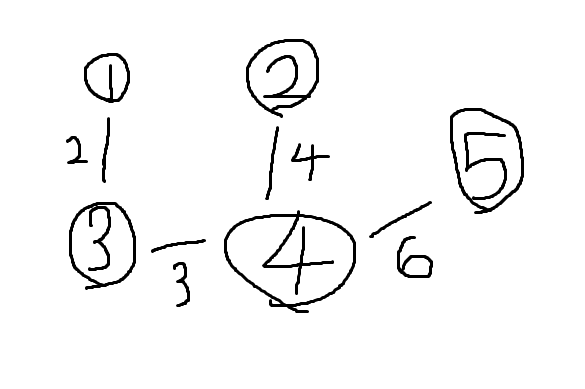
예제에 따라 이런 식으로 트리가 구성된다. 가장 긴 트리의 지름은 다음과 같다. 

트리 노드의 구성

트리 지름

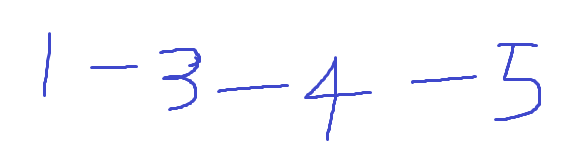
따라서 트리의 지름이 11이 된다. 코드는 다음과 같다.

from collections import defaultdict

def dfs(start, edges) :
    # 시작 노드와 거리를 스택에 넣고 초기화
    visited = [-1] * (V + 1)
    stack = [(start, 0)]
    visited[start] = 1

    while stack :
        # 스택에서 노드와 현재까지의 거리를 꺼냄
        node, dist = stack.pop()
        for nxt_node, nxt_dist in edges[node] :
            # 방문하지 않은 인접 노드를 찾음.
            if visited[nxt_node] == -1 :
                # 새 노드까지의 거리를 계산하고 저장
                visited[nxt_node] = dist + nxt_dist
                # 새 노드와 그 거리를 스택에 추가
                stack.append((nxt_node, visited[nxt_node]))

    return visited

# 노드의 개수 입력
V = int(input())
# 각 노드의 인접 리스트를 저장할 배열 초기화
edges = defaultdict(list)

# 트리 정보 입력 받기
for _ in range(V) :
    edge = list(map(int, input().split()))[:-1]
    # 인접한 노드와 거리 정보를 edges에 저장
    for i in range(1, len(edge) - 1, 2) :
        edges[edge[0]].append((edge[i], edge[i+1]))

# 첫 번째 DFS : 임의의 노드(여기서는 1)에서 가장 먼 노드를 찾기
ans = dfs(1, edges)
# 가장 먼 노드의 인덱스 찾기
max_node = ans.index(max(ans))

# 두 번째 DFS : 가장 먼 노드에서 시작하여 트리의 지름 찾기
res = dfs(max_node, edges)
# 트리의 지름 출력
print(max(res))

지금 이 글을 적는 지금까지 왜 DFS를 두 번 동작시키는지 이해가 잘 가지 않는다.