[Gold III] 파티 - 1238
성능 요약
메모리: 112912 KB, 시간: 208 ms
분류
데이크스트라, 그래프 이론, 최단 경로
제출 일자
2024년 3월 10일 00:18:27
문제 설명
N개의 숫자로 구분된 각각의 마을에 한 명의 학생이 살고 있다.
어느 날 이 N명의 학생이 X (1 ≤ X ≤ N)번 마을에 모여서 파티를 벌이기로 했다. 이 마을 사이에는 총 M개의 단방향 도로들이 있고 i번째 길을 지나는데 Ti(1 ≤ Ti ≤ 100)의 시간을 소비한다.
각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다. 하지만 이 학생들은 워낙 게을러서 최단 시간에 오고 가기를 원한다.
이 도로들은 단방향이기 때문에 아마 그들이 오고 가는 길이 다를지도 모른다. N명의 학생들 중 오고 가는데 가장 많은 시간을 소비하는 학생은 누구일지 구하여라.
입력
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어온다. 시작점과 끝점이 같은 도로는 없으며, 시작점과 한 도시 A에서 다른 도시 B로 가는 도로의 개수는 최대 1개이다.
모든 학생들은 집에서 X에 갈수 있고, X에서 집으로 돌아올 수 있는 데이터만 입력으로 주어진다.
출력
첫 번째 줄에 N명의 학생들 중 오고 가는데 가장 오래 걸리는 학생의 소요시간을 출력한다.
풀이
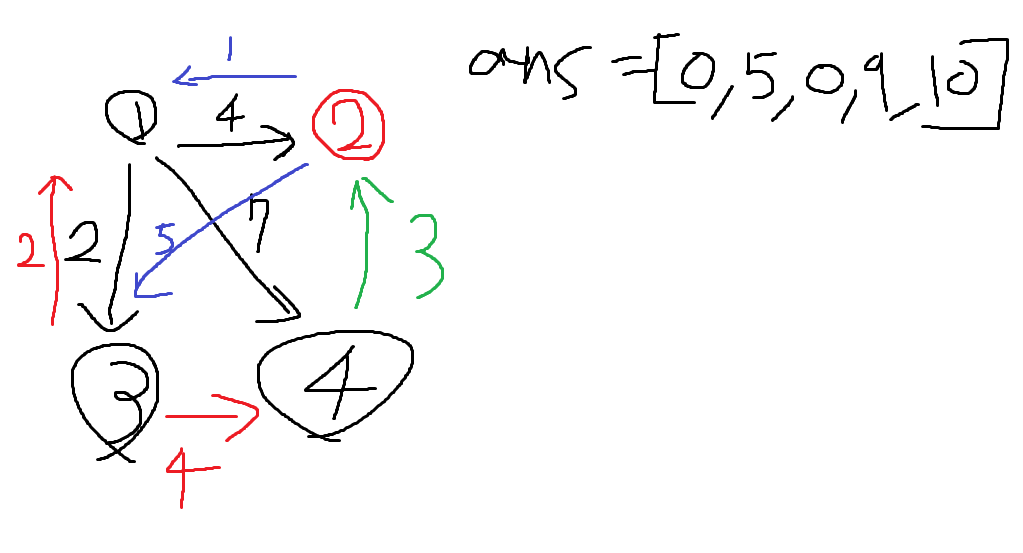
# 다익스트라 함수
def dijkstra(start, edges) :
distances = [float('inf')] * (N + 1) # 모든 노드의 거리를 무한대로 초기화
distances[start] = 0 # start는 0으로 초기화
q = []
heapq.heappush(q, [start, distances[start]]) # 우선순위 큐를 활용하여 start와 그 거리(0)을 입력
while q :
current_node, current_distance = heapq.heappop(q) # 데이터 출력
if distances[current_node] < current_distance : # 기존 거리가 더 적은 경우 통과
continue
for adj, weight in edges[current_node] :
dist = current_distance + weight # 현재 거리에 weight를 더함
if dist < distances[adj] : # dist가 다음 노드까지 거리보다 적은 경우
distances[adj] = dist # 갱신
heapq.heappush(q, [adj, dist]) # 다시 우선순위 큐에 입력
return distances # 모든 노드에 대한 시작 노드의 최단 거리 반환
# 데이터 입력
N, M, X = map(int, input().split())
edges = defaultdict(list) # 정방향 다익스트라 그래프 초기화
r_edges = defaultdict(list) # 역방향 다익스트라 그래프 초기화
for _ in range(M) :
A, B, T = map(int, input().split())
edges[A].append((B, T)) # 정방향 다익스트라 그래프 저장
r_edges[B].append((A, T)) # 역방향 다익스트라 그래프 저장
to_x = dijkstra(X, edges) # 정방향 다익스트라
from_x = dijkstra(X, r_edges) # 역방향 다익스트라
# 최대 왕복 시간 구하기
ans = 0
for i in range(1, N + 1) :
ans = max(ans, to_x[i] + from_x[i])
print(ans)해당 풀이는 ChatGPT를 이용하여 확보하였다.
- 코드의 목적
- 특정 노드 X에서 다른 노드까지의 왕복 시간을 계산한 후, 최대 왕복 시간 찾기
- 사용된 개념
- 다익스트라 알고리즘
- 우선순위 큐(heapq)를 사용하여 최단 경로를 계산
- edges와 r_edges를 통해 단방향 간선을 저장
- 그래프 구조
- edges : 정방향 간선을 저장(출발 -> 도착).
- r_edges : 역방향 간선을 저장 (도착 -> 출발)
- 왕복 시간 계산
- X에서 다른 노드로 가는 시간(to_x)
- 다른 노드에서 X로 오는 시간 (from_x)
- 두 값을 더해서 왕복 시간 계산
- 다익스트라 알고리즘
- 시간 복잡도
- 다익스트라 알고리즘의 시간 복잡도: O(E logV)
(E: 간선 수, V: 노드 수) - 정방향 다익스트라와 역방향 다익스트라를 각각 수행하므로 :
O(2 * E logV) ~= O(E logV)
- 다익스트라 알고리즘의 시간 복잡도: O(E logV)
- 핵심 포인트
- 정방향과 역방향 그래프를 구분해서 최단 경로를 계산
- 우선순위 큐를 사용해 다익스트라의 효율성을 높였다.
- 왕복 최단 경로를 계산하여 최대 왕복 시간을 구함.
코드 흐름 분석
1. 입력 처리
# 데이터 입력
N, M, X = map(int, input().split())
edges = defaultdict(list) # 정방향 다익스트라 그래프 초기화
r_edges = defaultdict(list) # 역방향 다익스트라 그래프 초기화
for _ in range(M) :
A, B, T = map(int, input().split())
edges[A].append((B, T)) # 정방향 다익스트라 그래프 저장
r_edges[B].append((A, T)) # 역방향 다익스트라 그래프 저장- N : 노드 개수
- M : 간선 개수
- X : 기준 노드
- edges에는 정방향 간선을 저장
- r_edges에는 역방향 간선을 저장
2. 다익스트라 함수(dijkstra)
def dijkstra(start, edges) :
distances = [float('inf')] * (N + 1) # 모든 노드의 거리를 무한대로 초기화
distances[start] = 0 # start는 0으로 초기화
q = []
heapq.heappush(q, [start, distances[start]]) # 우선순위 큐를 활용하여 start와 그 거리(0)을 입력
while q :
current_node, current_distance = heapq.heappop(q) # 데이터 출력
if distances[current_node] < current_distance : # 기존 거리가 더 적은 경우 통과
continue
for adj, weight in edges[current_node] :
dist = current_distance + weight # 현재 거리에 weight를 더함
if dist < distances[adj] : # dist가 다음 노드까지 거리보다 적은 경우
distances[adj] = dist # 갱신
heapq.heappush(q, [adj, dist]) # 다시 우선순위 큐에 입력
return distances # 모든 노드에 대한 시작 노드의 최단 거리 반환- 거리 배열 distances를 초기화하고, 우선순위 큐를 통해 최단 경로를 계산
- 각 노드에서 인접한 노드를 탐색하며 최단 거리 업데이트 (dist)
3. 정방향 및 역방향 다익스트라 실행
to_x = dijkstra(X, edges) # 다른 노드 → X로 가는 최단 경로
from_x = dijkstra(X, r_edges) # X → 다른 노드로 가는 최단 경로4. 최대 왕복 시간 계산
# 최대 왕복 시간 구하기
ans = 0
for i in range(1, N + 1) :
ans = max(ans, to_x[i] + from_x[i])
print(ans)